فرمول های ریاضی محاسبه محیط و مساحت و حجم چند ضلعی ها (اشکال هندسی)
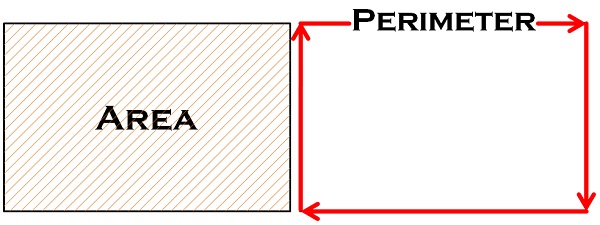
در هندسه، اجتماع حداقل سه پاره خط که همگی در یک صفحه قرار دارند و هر پاره خط درست دو پاره خط دیگر را در نقاط انتهایی آن قطع کند، چند ضلعی نام دارد. هر چند ضلعی یک محیط و مساحت قابل محاسبه دارد. محیط دور تا دور چند ضلعی است و مساحت داخل چند ضلعی می باشد. بطورکلی مساحت یعنی با چند مربع می توان سطح یک شکل هندسی را پوشاند، و اگر دور یک شکل هندسی را حصار بکشیم (مثلاً با نخ) و سپس طول آن حصار را اندازه بگیریم (مثلاً طول نخ را)، محیط شکل هندسی بدست می آید.
در این مقاله شما می توانید با فرمول های ریاضی محاسبه محیط و مساحت و حجم چند ضلعی ها و سایر اشکال هندسی آشنا شوید.
مربع
| مربع یا چهار ضلعی منتظم، شکلی هندسی است که اندازه همه اضلاع آن برابر باشد و هر ضلع با هم زاویه 90 درجه می سازند. | |
| محیط: یک ضلع × 4 مساحت: یک ضلع × خودش یا طول × عرض | |
مستطیل
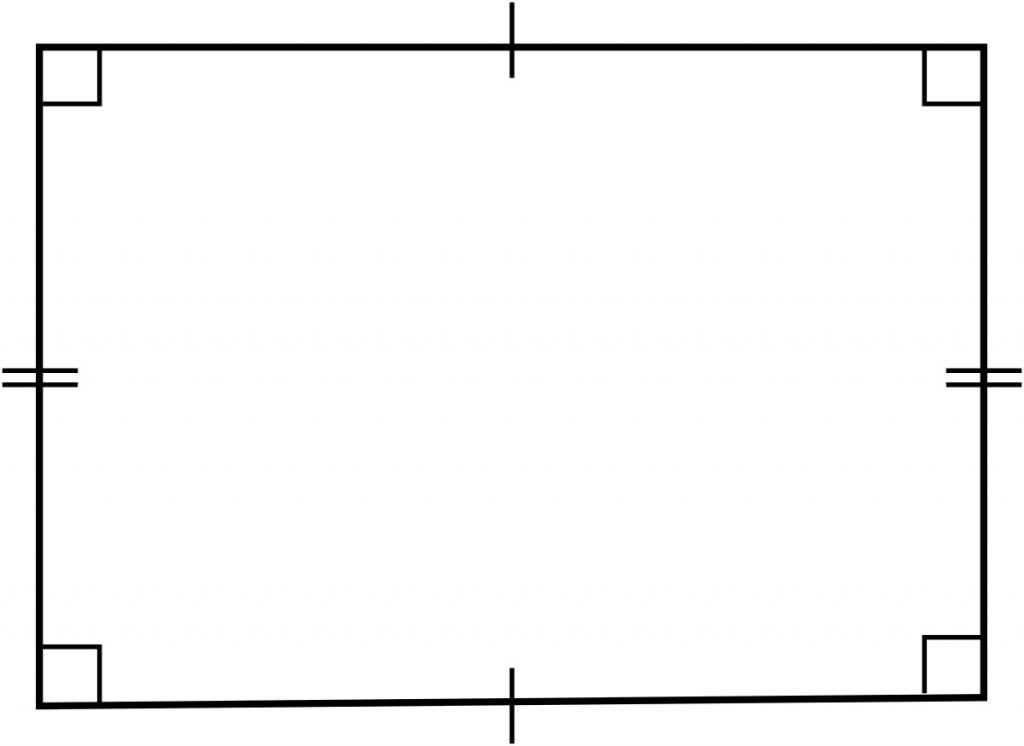
| مستطیل شکلی هندسی است که تمام زوایای آن قائمه باشد. | |
| محیط: (طول + عرض) × 2 مساحت: طول × عرض | |
مثلث
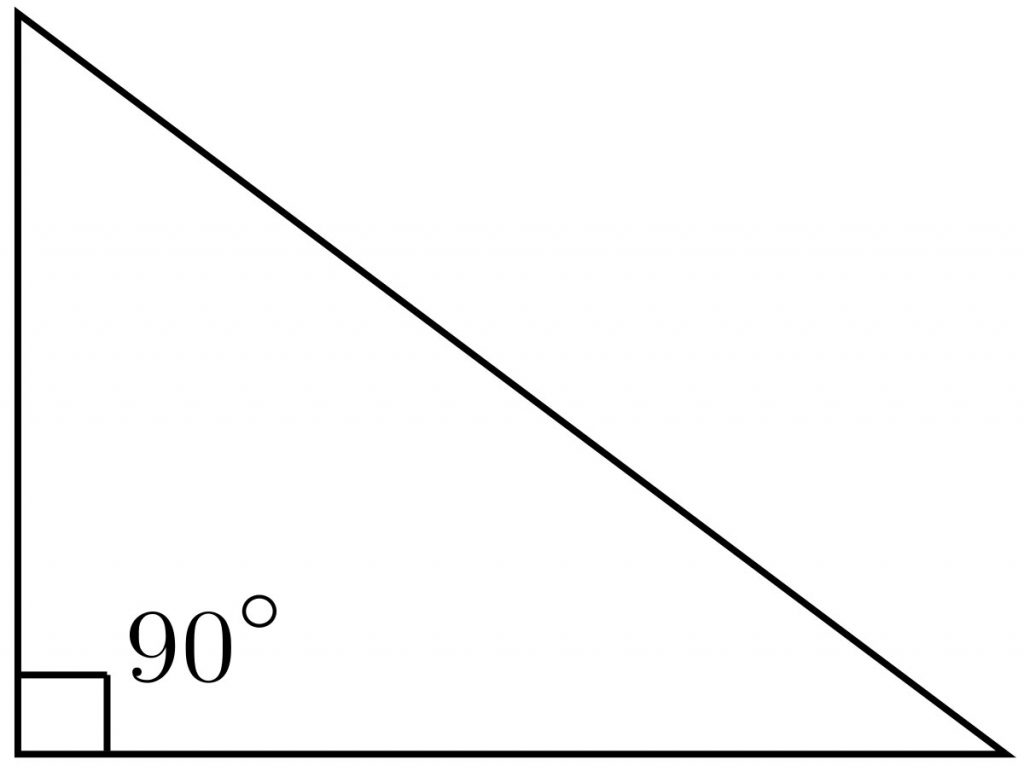
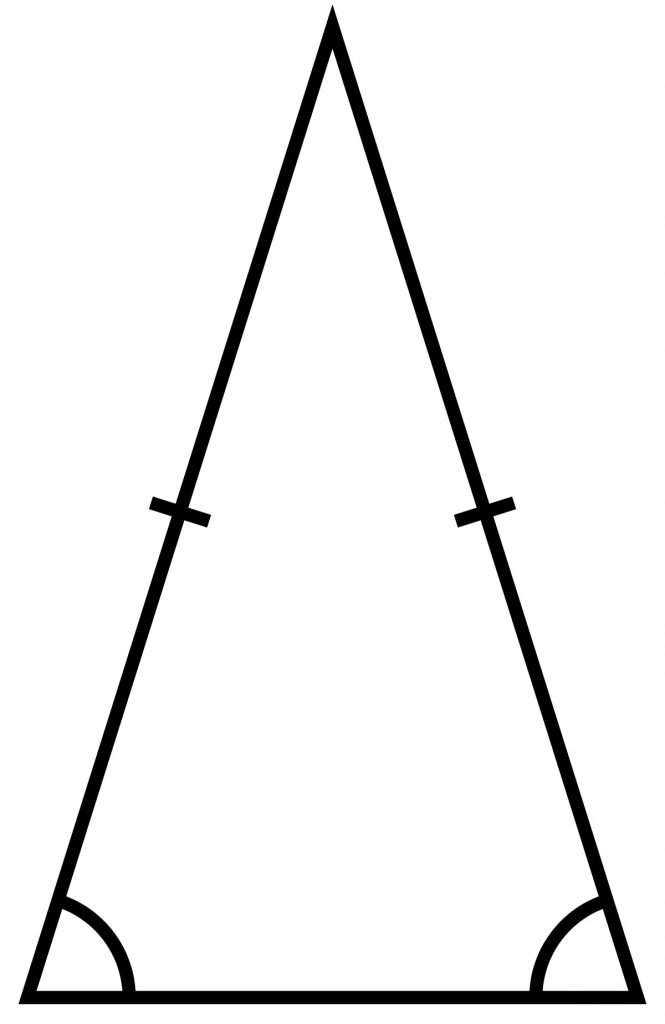
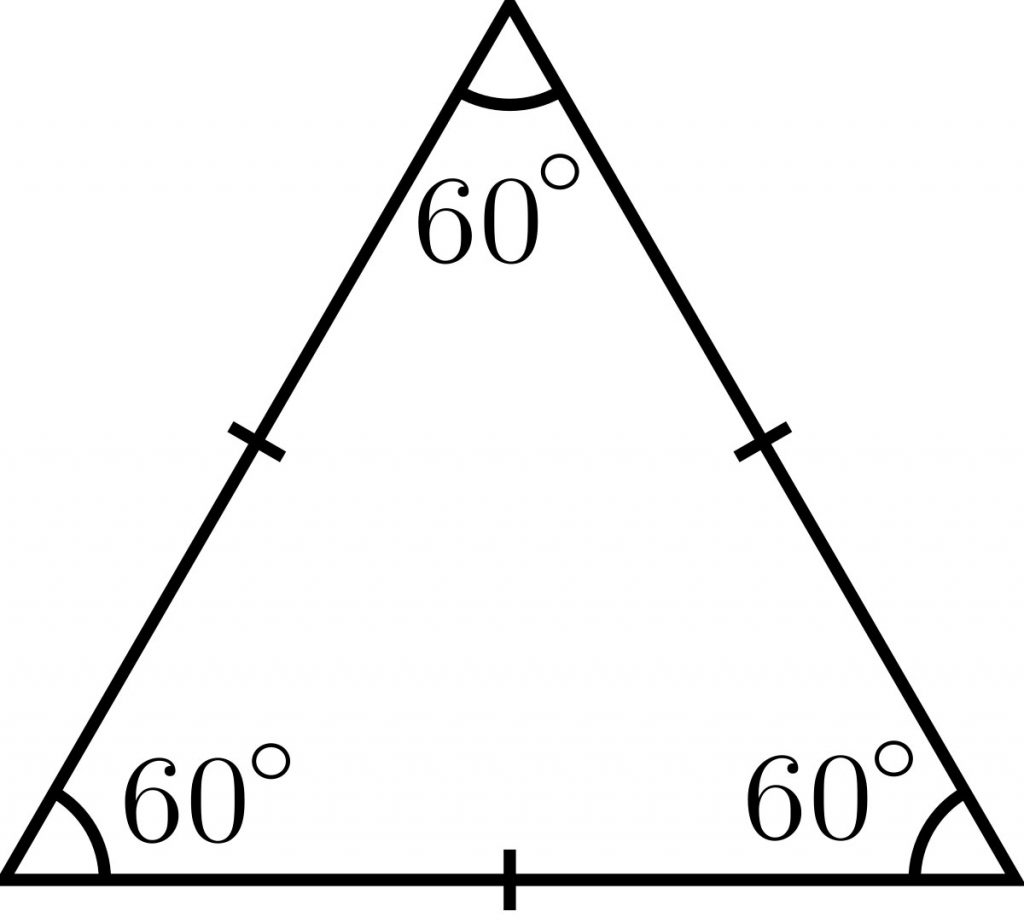
| مثلث شکلی هندسی است که سه ضلع دارد.
| |
| محیط: مجموع سه ضلع مساحت: (قاعده × ارتفاع) ÷ 2 | |
ذوزنقه
| ذوزنقه شکلی هندسی است که چهار ضلع دارد که دو ضلع آن موازی هستند. | |
| محیط: مجموع چهار ضلع مساحت: ارتفاع × (قاعده بزرگ + قاعده کوچک) ÷ 2 | |
متوازی الاضلاع
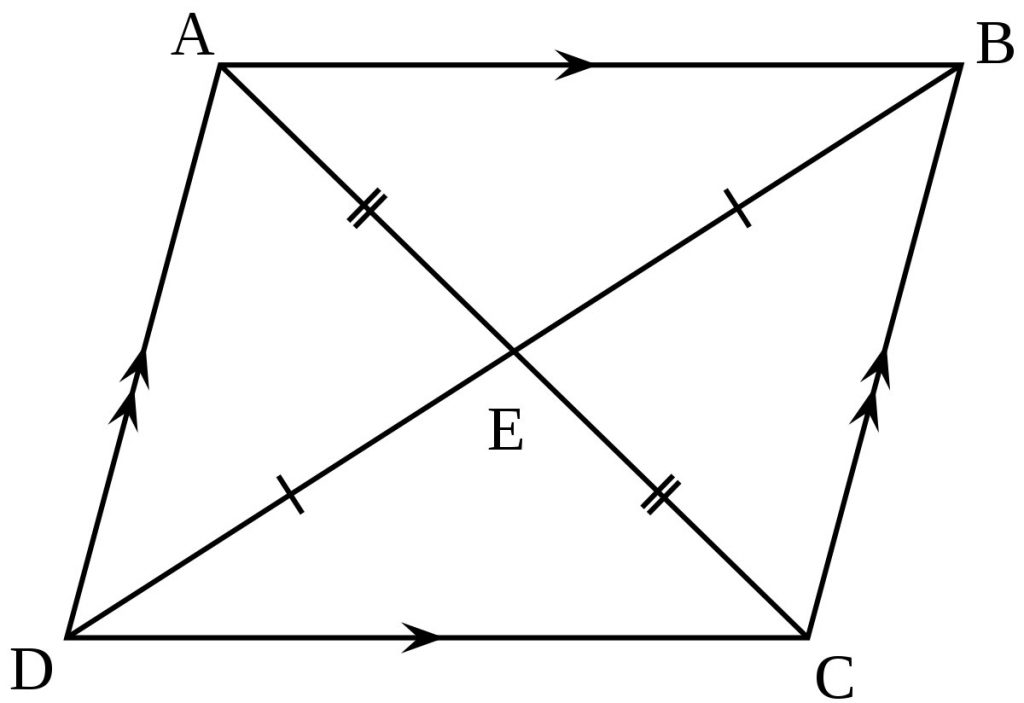
| متوازی الاضلاع شکلی هندسی است که اندازه اضلاع و زوایای روبروی یکدیگر با هم برابر است. | |
| محیط: مجموع دو ضلع متوالی × 2 مساحت: ارتفاع × قاعده | |
لوزی
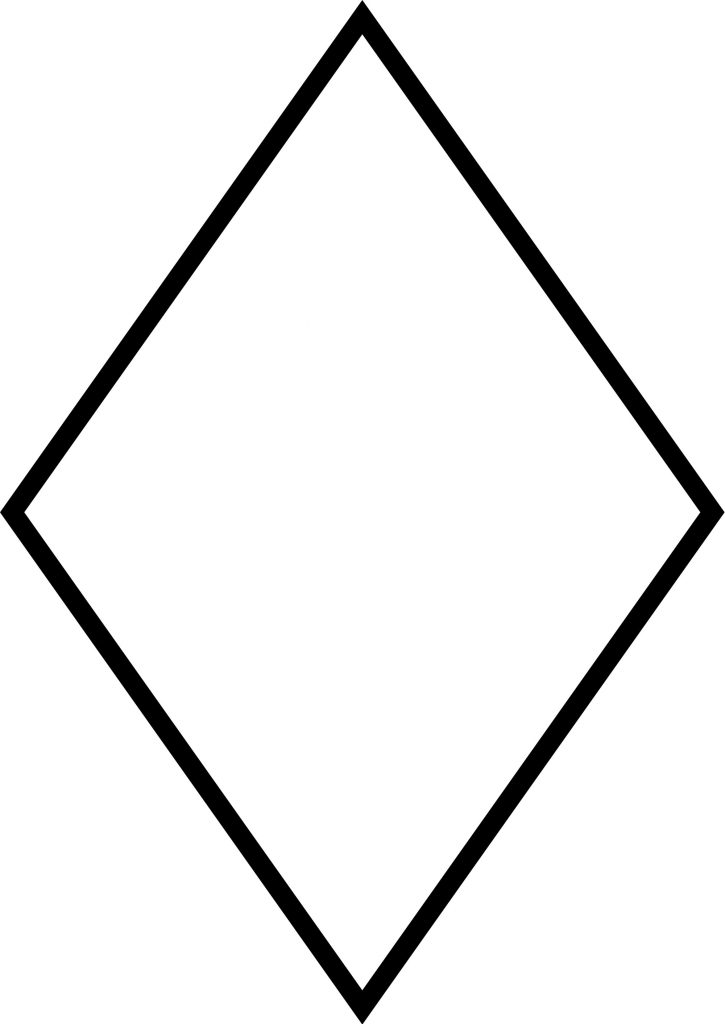
| لوزی شکلی هندسی با چهار ضلع است که اضلاعش با هم برابر می باشند. به عبارتی لوزی، متوازی الاضلاعی است که قطرهای آن بر هم عمود باشند. | |
| محیط: یک ضلع × 4 مساحت: (قطر بزرگ × قطر کوچک) ÷ 2 | |
بیضی
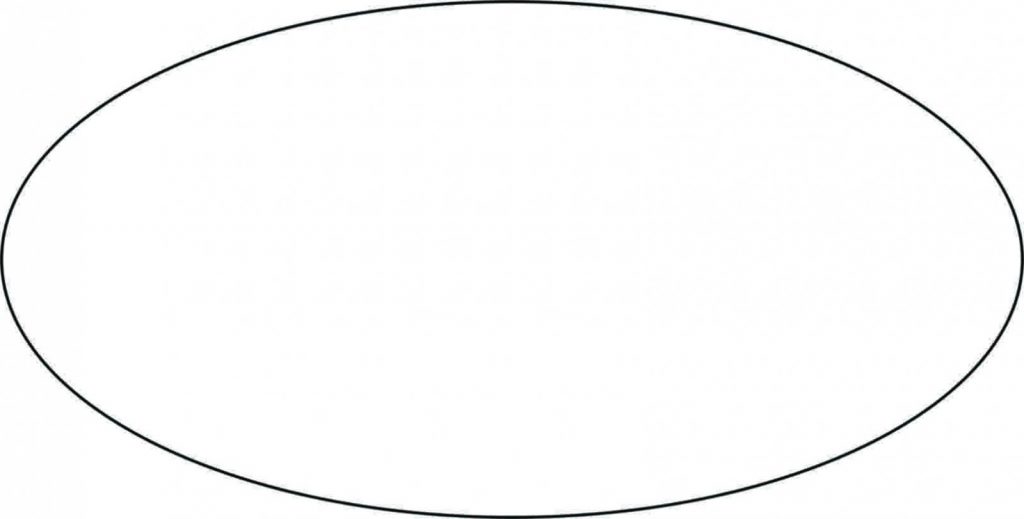
| بیضی شکلی هندسی است که مکان هندسی نقاطی از صفحه که مجموع فاصله های آنها از دو نقطه ثابت مساوی با ثابتی مثبت باشد. | |
| مساحت: (نصف قطر بزرگ × نصف قطر کوچک) × π π = 3.14 | |
دایره
| دایره نوعی بیضی است که مکان هندسی نقاطی از صفحه که فاصله شان از نقطه ثابتی واقع در آن صفحه، مقدار ثابتی باشد. | |
| محیط: قطر × π قطر: شعاع × 2 مساحت: شعاع × شعاع × π | |
کره
| کره یک شکل هندسی کاملاً گرد در فضای سه بعدی است. تمامی نقاطی که بر سطح کره جای دارند، در فاصله یکسان از مرکز کره قرار دارند. | |
| حجم: مساحت: 4 × π × شعاع به توان 2 | |
چند ضلعی منتظم
| چند ضلعی منتظم، چندضلعی است که همه زوایا و اضلاع آن هم اندازه هستند. | |||
| محیط: طول یک ضلع × تعداد اضلاع مساحت: از روابط زیر بدست می آید.
| |||
مکعب مربع
| مکعب مربع به شکل هندسی سه بعدی گویند که از 6 مربع برابر تشکیل شده باشد. به صورتی که هر ضلع هر یک از مربع ها با تنها یک مربع دیگر مشترک باشد و در راس ها سه مربع با یکدیگر در ارتباط هستند. مکعب را می توان یک شش وجهی منظم نامید. | |
| حجم: مساحت قاعده × ارتفاع یا یک ضلع به توان 3 مساحت: یک ضلع به توان 2 × 6 | |
مکعب مستطیل
| مکعب مستطیل یک شکل هندسی سه بعدی است که دارای شش وجه مستطیل شکل است. همچنین دارای 8 گوشه و 12 لبه است. در مکعب مستطیل همه زوایا قائمه و وجوه روبروی هم با یکدیگر برابر می باشند. | |
| طول = a حجم: a × b × c مساحت: 2ab + 2ac + 2bc | |
هرم
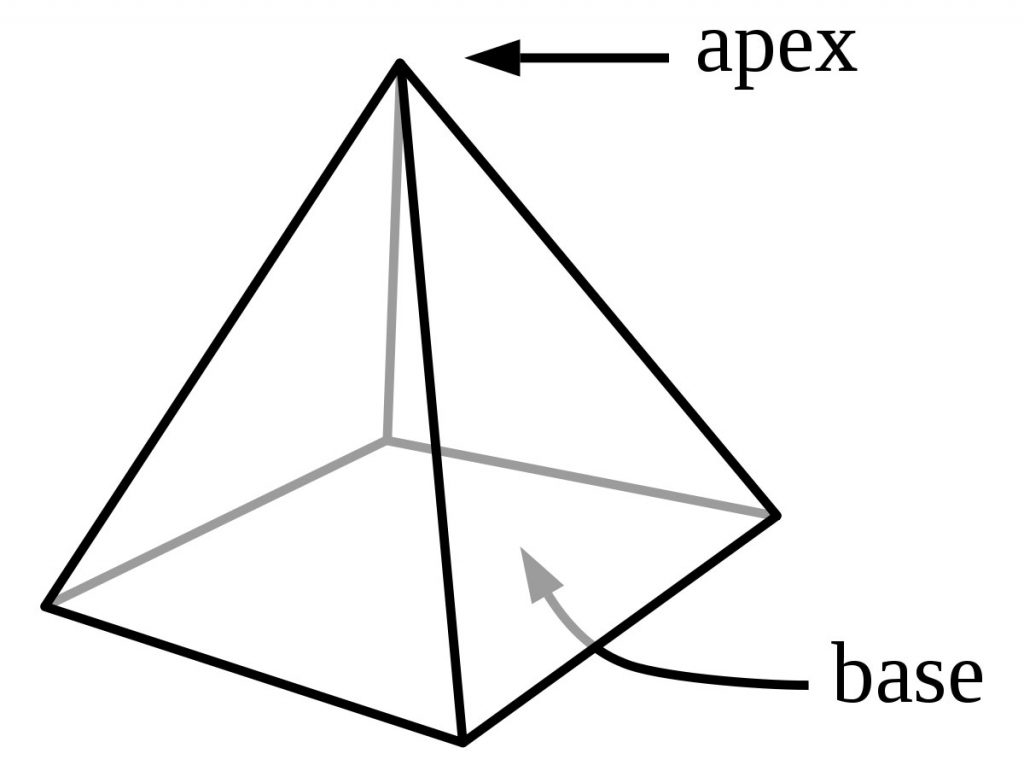
| هرم شکلی سه بعدی است که از اتصال نقطه ای در فضا به تمام نقاط شکلی بسته در صفحه به وجود می آید. به آن نقطه، راس هرم و به آن شکل مسطح، قاعده هرم گفته می شود. | |
| حجم: ارتفاع هرم × مساحت قاعده هرم × | |
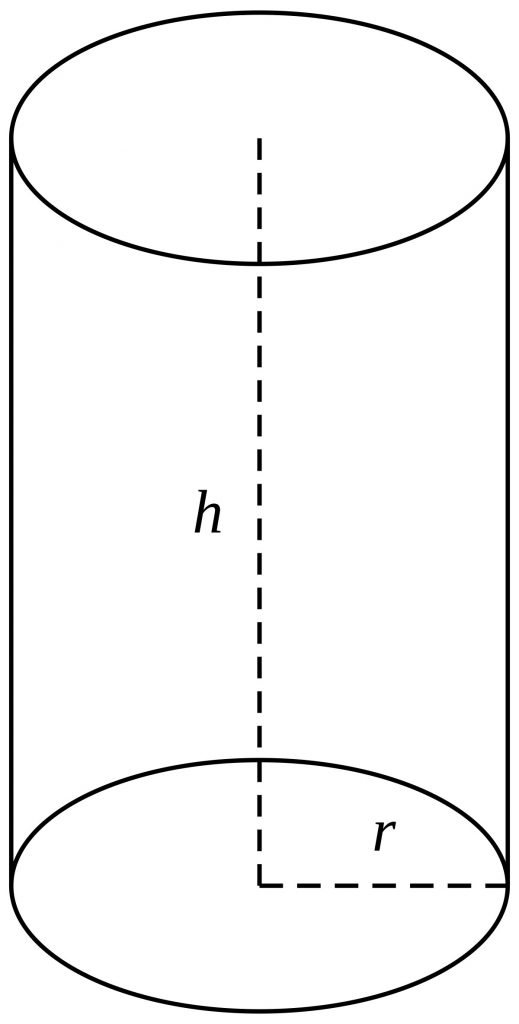
استوانه
| استوانه شکلی هندسی است که سطح دور آن را مجموعه نقاطی تشکیل می دهد که در فاصله یکسان از یک خط راست قرار دارند، این خط راست محور نام دارد. دو سر این شکل فضایی به کمک دو صفحه عمود بر محور استوانه بسته می شود. | |
| مساحت جانبی: محیط قاعده × ارتفاع حجم: مساحت قاعده × ارتفاع سطح کل استوانه: مساحت دو قاعده + مساحت جانبی | |
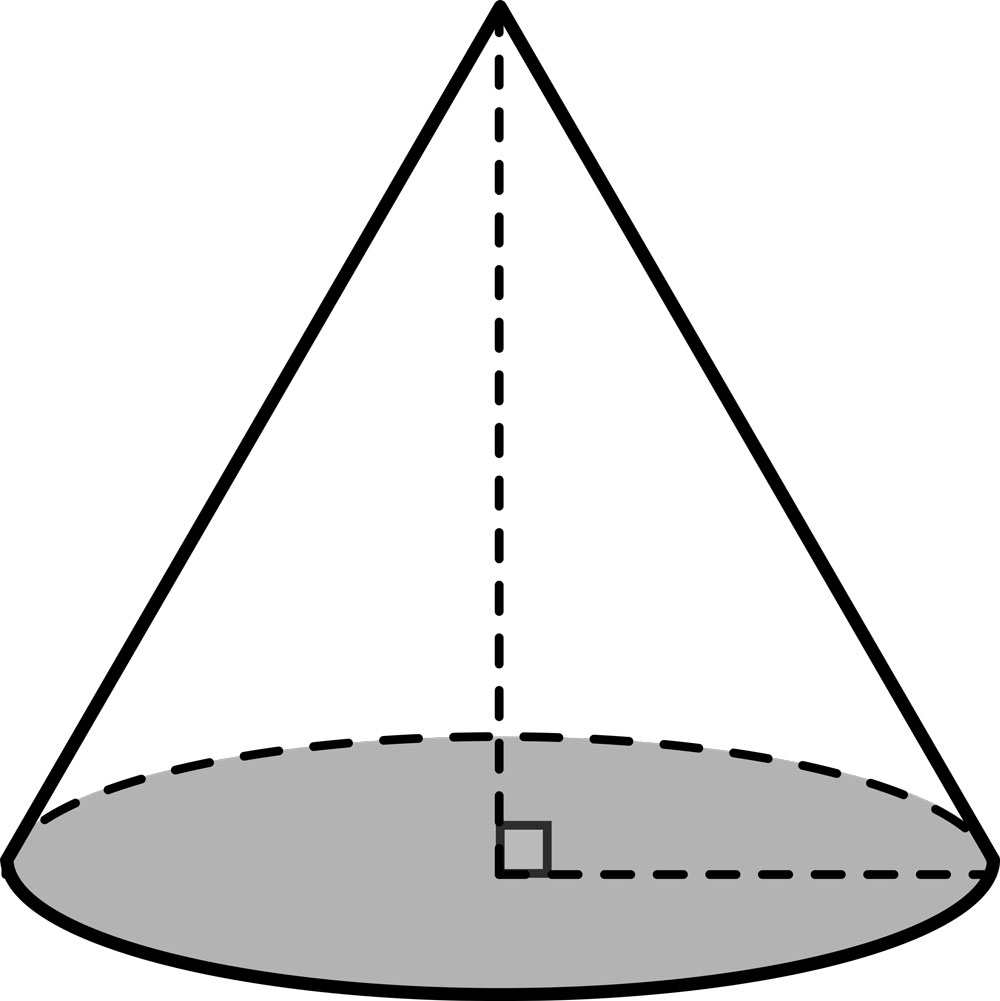
مخروط
| مخروط یکی از گونه های هرم است که قاعده آن دایره است. | |
| حجم: مساحت قاعده × ارتفاع × | |




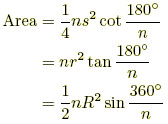






سلام میشه بگین محیط چهار ضلعی چه عددی است
ممنون میشم اگه بکین
مساحت و یک ۳۵ ضلعی منظم، هر ضلع ۵ به ارتفاع ۱۰ چجوری به دست میاد؟
سلام فرمول بدست آوردن پنج ضلعی منتظم چیه؟
ممنون میشم اگه بگید?
از نظر عددی وقتی ضلع مربع ۴ باشد محیط برابر است با ۱۶ متر و مساحت می شود ۱۶ متر مربع که از لحاظ مفهومی متفاوت هستند چون مساحت مقدار سطح بر متر مربع را میدهد
چه زمانی محیط و مساحت یک مربع برابر است چرا
محیط مربع = 4a
مساحت مربع = a^2
4a=a^2
a^2-4a=0
a(a-4)=0
a=0 و a=4
محیط و مساحت یک مربع زمانی با هم برابر هستند که اندازه اضلاع مربع برابر با 4 باشند. به دلایل فوق.
مساحت ۶ ظلعی منظم چیست؟
هر زاویه ۶ ضلعی منتظم برابر است با ۱۲۰ درجه اگر نقطه وسط ۶ ضلعی را در نظر بگیریم و با ۶ خط به زوایای ۶ ضلعی وصل کنیم ۶ مثلث برابر متساوی الاضلاع بدست می آوریم کافی است مساحت یک مثلث را بدست آوریم و در ۶ ضرب کنیم اگر ارتفاع را h و هر ضلع ۶ ضلعی را a بگیربم مساحت هر مثلث میشود 1/2× a×h پس مساحت ۶ ضلعی میشود 3ah
سلام میخواستم بدونم مساحت یک نمازخانه به شکل هشت ضلعی چجوری بدست می آید ؟؟
سلام. برای بدست آوردن دو دایره که تودتو هستند مساحت و محیط دایره کوچک را چگونه بدست بیاوریم در حالی که ما فقط مقدار اضافی که دایره کوچک را اشغال نکرده را داریم که مقدار اضافه دو طرف دو تا ده تا و عرض اضافه 18 است.
چطور مساحت ۵ضلعی رو به دست بیاریم
من هم سوالم همینه
با عرض سلام و خسته نباشید،
میخواستم بدونم مساحت یک چهار ضلعی که اندازه هر چهار ضلعش متفاوت است چطوری محاسبه میشود.
با سپاس فراوان
خوب اگر اضلاع باهم مساوی باشد هر دو ضلع را باهم ضرب کن یعنی مربع انها. اگر اضلاع با هم مساوی نباشد باز هم هر دو ضلع را با هم ضرب کن ولی این بار دو عدد متفاوت خواهد بود. در حالت اول اینطور خواهیم داشت a×a. ولی در حالت دوم عوض b,a خواهد بود که همان عدد دومی استش.
با سلام
۰/۸محیط مربع بود اگر نصف ان محیط لوزی باشد اندازه هر ضلع ان چند است؟
یک سوال چگونه می توان حجم مکعب را با استفاده از قطرش بدست اورد؟ فرمولش چیست؟
قطرش رو ÷رادیکال ۳ کن
ضلعش به دست میاد
ضلع رو به توان ۳ برسون
ببخشید کسی میدونه با ۱۶ مکعب واحد میشه چند تا مکعب مستطیل مختلف ساخت و با ۲۴ تا میشه چند تا ساخت؟
از طریق مساحت دایره چگونه محیطش را بدست آوریم؟
اول تقسیم بر پی یا 3.14 میکنیم سپس رادیکال میگیریم عدد به دست آمده شعاع میباشد سپس محیط را حساب میکنیم
سلام ببخشید این سوال را کسی بلده
محیط یک لوزی ۲۰ است قطر بزرگ ۸ قطر کوچک چند است
طول یه ضلع میشه 20/4 یعنی 5. حالا نصف قطر بزرگ و قطر کوچک و یک ضلع یه مثلث قائم الزاویه میشه. در این صورت نصف قطر کوچک میشه 3. قطر کوچک مساوی 6 میشه
سلام. قطر بزرگ رو نصف کن میشه 4. بعد 20 رو تقسیم بر 4 کن تا ضلع لوزی بدست بیاد که میشه 5. بعد از رابطه a2+b2=c2 میریم که میشه 16+b2=25 که b=3. عددبدست آمده در اصل نصف قطر کوچک است ??
لوزی رو که بکشین یه ضلع 5 هست نصف قطر بزرگ 4 پس فیثاغورس میرنین نصف قطر کوچیک میشه 3 کلش میشه 6
سلام
مساحت يك باغچه را كه غير هندسي متداول است ولي محيط آن را با پيمايش ميتوان اندازه گيري كرد چگونه بدست اوريم
انتگرال
چگونه از روی قطر مربع مساحت را پیدا کنیم
نصف مجذور قطر
قطر×قطر÷۲
بدست آوردن مساحت مربع از روش لوزی
آقا مساحت مربع میشه (یک ضلع×خودش) مربع که عرض نداره???
عرض و طول مربع با هم برابرند کی گفت که عرض نداره
بسیار عالی و ممنون
اق مساحت پنج ضلعی چی شد په ما یه ساعت دنبالش بودیم اخرشم پیدا نکردیم ???
مساحت هر nضلعی منتظم میشه nضربدر مساحت مثلث متساوی الاضلاع که اون خودش میشه جذر سه روی چهار
مساحت چهار ضلعی مختلف الاضلاع چه جوری بدست میاد؟ ?
ببخشید مساحت های چند ضلعی منتظم چگونه حساب میشه??
همکلاسی و همراه خوب یو سی؛ هانیه عزیز
با سلام و احترام
به متن اضافه گردید.
مساحت 5 ضلعی چه جوریه؟؟؟؟
ببخشید میشه مساحت هرم رو واسم بگین
میشه شعاع دیگه
سلام.. میشه بگید زاویه یه مخروط رو چطوری به دست میارن… منظورم فرمولشه
مساحت مکعب چیه
سلام. مکعب چون دارای شش وجه یا قسمت هست مساحت و اندازه یک قسمت را به دست می آوریم و در 6 ضرب می کنیم. مثلا اگر مساحت یک وجه مکعب 16 باشد، 16 در 6 ضرب میکنیم.
مساحت یک وجه*6
سلام
اندازه ى يك وجه مربع رو پيدا من بعد در ٦ ضرب كن
مثال: مساحت مكعبى كه اندازه ى يك ضلع ٣ هست را بياييد
3 در ٣ ضرب ميشه كه جواب ميشه ٩ بعد ٩ در ٦ ضرب كن كه ميش ٥٤
ببخشید من اخر محیط و مساحت شش ضلعی و هشت ضلعی رو ندیدم و متوجه نشدم
با سلام و عرض ادب
مساحت لوزی میشه (قطر بزرگ * قطر کوچک)/2
همکلاسی و همراه خوب یو سی؛ بهادری عزیز
با سلام و تشکر از اطلاع رسانی شما
اطلاح شد.
اندازه یک ضلع هشت ضلعی که ارتفاع مثلث های قائم زاویه آنها ۲۴ است چه اندازه میشود؟