خیام؛ پیشگام کشفیات ریاضی

شاید در متون ریاضی به نام هایی چون «چهار ضلعی خیام – ساکری»، «مثلث خیام – پاسکال» و «دو جمله ای خیام – نیوتن» برخورد کرده و این سوال به ذهن تان خطور کرده باشد که به چه دلیل نام خیام در کنار ریاضیدان ها و دانشمندانی قرار گرفته است که چندین قرن پس از او می زیسته اند؟ شاید هم به درستی حدس زده اید که خیام حتماً سهمی در دستاوردهای دانشمندان یاد شده داشته است.

غیاث الدین ابوالفتح عمر بن ابراهیم خیام نیشابوری حدود سال 427 شمسی در نیشابور به دنیا آمده و در 510 شمسی در زادگاه خود درگذشته است. در نزد امام موفق شیرازی، از علما و دانشمندان مشهور آن زمان در نیشابور، فقه، تفسیر، فلسفه و ستاره شناسی آموخت.

خیام خود را از شاگردان ابن سینا دانسته است اما با توجه به اینکه بوعلی چندین سال قبل از تولد او فوت کرده بود، مشخص می شود که این سخن به دل بستگی خیام به افکار ابن سینا اشاره دارد. از این رو او را از لحاظ فلسفی پیرو فلسفه مشائی ابن سینا می دانند. خیام در علوم زمانه خود به استادی رسید و چنانچه در ادامه خواهید خواند او در برخی مباحث ریاضی از زمانه خود قرن ها پیش افتاد.

در این مقاله شما می توانید با خیام، نابغه پیشگام در ریاضیات آشنا شوید.

رساله خیام در شرح مشکلات کتاب اصول اقلیدس
با اینکه در رساله های به جا مانده از خیام، آثاری در فلسفه، نظریه ریاضی موسیقی، مکانیک و تعیین وزن مخصوص اجسام و هواشناسی دیده می شود اما آنچه او را در تاریخ علم برجسته می سازد، تحقیقات او در هندسه اقلیدسی و ابداعاتش در حل معادلات درجه سوم است. خیام در رساله فی شرح ما اشکال من مصادرات اقلیدس (در شرح مشکلات کتاب اصول اقلیدس) به بررسی اصول هندسه اقلیدسی پرداخت. نسخه دست نویس این کتاب در کتابخانه برلین نگهداری می شود و تاریخ نگارش آن اواخر جمادی الاول سال 470 هجری قمری ذکر شده است. اقلیدس که سعی کرد ضمن جمع آوری قضایای هندسی موجود، به اثبات برهانی آنها بپردازد، با چهار اصل اولی که فرض کرد، توانست 28 قضیه هندسی را اثبات کند اما برای اثبات قضایای بیشتر مجبور شد اصل پنجمی را نیز اضافه کند.

تشکیک خیام در اصل توازی اقلیدس
چند مسئله باعث شد که پذیرش اصل پنجم یا اصل توازی برای ریاضیدانان بعدی دشوار باشد. یکی اینکه این اصل بداهت و ایجاز چهار اصل اول را نداشت. دوم اینکه این اصل بیشتر به یک قضیه شباهت داشت تا یک اصل موضوعه. سوم اینکه اقلیدس پس از اثبات 28 قضیه با چهار اصل اول و ناکامی در اثبات قضایای بیشتر با آن اصول و 28 قضیه اثبات شده، ناگزیر به افزودن اصل پنجم شد.

پس از اقلیدس ریاضیدانان بسیاری سعی کردند این اصل آزاردهنده را با استفاده از چهار اصل اول به اثبات برسانند. خیام در رساله در شرح مشکلات کتاب اصول اقلیدس سعی کرد اصل توازی را اثبات کند. روشی که خیام برای این منظور بکار گرفت 700 سال بعد مورد توجه ریاضیدانان اروپایی قرار گرفت.

ابداع روشی هندسی برای حل معادلات درجه سوم
با اینکه حل برخی معادلات خطی، قدمتی بیش از 3000 سال دارد و به مصر و بابل آن عصر بر می گردد و بعدها در هند و یونان نیز پیشرفت هایی در آن زمینه حاصل شد اما این کتاب جبر و مقابله خوارزمی در قرن نهم میلادی بود که آن را به شکل یک علم سامان بخشید و مدون کرد. اروپاییان کلمه جبر (Algebra) را نیز از نام همین کتاب برای نامگذاری این علم جدید اخذ کردند. خوارزمی ضمن بررسی معادلات درجه اول و درجه دوم، به اثبات هندسی آنها نیز پرداخت. اما دو قرن پس از آن، کار بزرگ بعدی در جبر را خیام در کتابی با همان عنوان جبر و مقابله به انجام رساند. چنانکه جرج سارتن، مورخ معروف علم در کتابش با عنوان مقدمه ای بر تاریخ علم نوشت: «خیام اولین است که به تحقیق منظم علمی در معادلات درجه اول، دوم و سوم پرداخته و طبقه بندی تحسین برانگیزی از این معادلات ارائه کرده است.» از نظر سارتن رساله جبر و مقابله خیام که شامل این تحقیقات است «یکی از مهم ترین آثار ریاضی قرون وسطایی و احتمالاً برجسته ترین آنها است.» استفاده خیام از مقاطع مخروطی برای حل معادلات درجه سوم، او را به پیشگام تحولات بعدی در این زمینه بدل کرد.

پیشگامی خیام در جبر و هندسه
اهمیت کار خیام وقتی مشخص می شود که به این واقعیت توجه کنیم که در زمان او عددنویسی به صورت امروزی و تشکیل معادلات جبری با علائم و نمادهای ریاضی وجود نداشته است. از این رو به نحوی می توان خیام را پیشگام هندسه تحلیلی و تحقیقات ریاضی دانشمندانی چون دکارت، پاسکال و نیوتن به حساب آورد. شاید به دلیل این تاثیرگذاری بنیانی در تاریخ علم است که جرج سارتن نیمه دوم قرن یازدهم میلادی را عصر خیام نامیده است. با این حال در اینکه آیا ریاضیدانان اروپایی مستقیماً از روش هندسی خیام برای حل معادلات هندسی تاثیر پذیرفته اند یا نه، اختلاف نظر وجود دارد. اما به استناد رساله های در «شرح مشکلات کتاب اصول اقلیدس» و «جبر و مقابله»، در این واقعیت که خیام پیشگام مباحثی بوده که چندین قرن پس از او امثال ساکری، لباچفسکی، دکارت، پاسکال و نیوتن به آنها پرداخته اند، تردیدی وجود ندارد.

دو جمله ای خیام – نیوتن و مثلث خیام – پاسکال
آنچه را که امروز مثلث خیام – پاسکال می نامند، یکی از زیباترین آرایه های ریاضی است که در تاریخ ریاضیات، توجه ریاضیدانان بسیاری را جلب کرده است. خیام روشی جبری برای بدست آوردن ضرایب دو جمله ای (که امروزه به دو جمله ای خیام – نیوتن معروف است)، کشف کرد. کتاب مشکلات حساب که شامل اثبات روش خیام بود، تاکنون کشف نشده است اما در آثار خواجه نصیر طوسی که متاثر از روش خیام بوده، ضرایب تا توان 12 محاسبه شده است.

در قرن هفدهم بلز پاسکال، ریاضیدان فرانسوی، که معاصر نیوتن بود، روی این بسط و مثلث حسابی آن کار کرد. به آرایش مثلثی شکل ضرایب بسط دو جمله ای خیام – نیوتن، مثلث خیام – پاسکال گفته می شود. در مثلث خیام – پاسکال اعداد هر سطر مثلث، ضرایب بسط دو جمله ای خیام – نیوتن هستند. در مثلث خیام – پاسکال هر عدد از مجموع دو عدد بالای خود بدست می آید و مجموع اعداد هر سطر برابر توان های صفر تا n عدد 2 است.

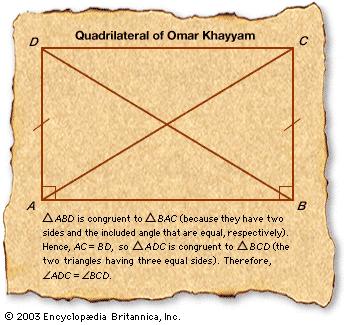
چهار ضلعی خیام – ساکری و پیدایش هندسه های نااقلیدسی
خیام برای اثبات اصل توازی، چهار ضلعی ABCD را فرض کرد که AD و BC دو پاره خط مساوی و هر دو بر AB عمود هستند. خیام می نویسد که برای اثبات اینکه اصل توازی از سایر اصول اقلیدس نتیجه می شود، کافی است ثابت گردد که زوایای داخلی C و D هر دو قائمه هستند. البته خیام مثل تمام ریاضیدانان بعدی، در این کار ناکام ماند اما این ناکامی ها در نهایت در قرن نوزدهم به تحولاتی بنیادی در هندسه منجر شد. بعدها خواجه نصیرالدین طوسی به بررسی نظریه خیام پرداخت و در قرن هیجدهم جیووانی ساکری، ریاضیدان ایتالیایی در کتابش با عنوان اقلیدس عاری از تناقض سعی کرد با طرح یک چهار ضلعی، شبیه به آنچه خیام فرض کرده بود، از طریق برهان خلف، اصل پنجم را از چهار اصل قبلی نتیجه بگیرد.

تمام سعی خیام، طوسی و ساکری این بود که اثبات کنند زوایای C و D نمی توانند جزء قائمه باشند و بنابراین سعی کردند فرض حاده یا منفرجه بودن آنها را رد کنند. در صورتی که با فرض اول به هندسه هذلولوی (هندسه لباچفسکی) و با فرض دوم به هندسه بیضوی (هندسه ریمانی) می رسیدند. در قرن نوزدهم برخی ریاضیدانان تلاش کردند خلاف اصل پنجم را فرض کنند تا ببینند که آیا به تناقض می رسند یا نه. وقتی هیچ تناقضی در هندسه های دارای اصل پنجم متفاوت، مشاهده نشد آنها را هندسه های نااقلیدسی نامیدند.

اصول موضوعه هندسه اقلیدسی
اصول موضوعه، فرضیاتی هستند که بدیهی شمرده شده و پذیرفته می شوند و مبنای اثبات سایر قضایا قرار می گیرند. اصول موضوعه هندسه اقلیدسی شامل پنج اصل زیر است:

• اصل اول: از هر دو نقطه فقط یک پاره خط مستقیم می گذرد.
• اصل دوم: هر پاره خط را می توان در امتداد آن بطور نامحدود ادامه داد.
• اصل سوم: برای هر پاره خط دلخواه، می توان دایره ای به شعاع آن پاره خط و به مرکز یک سر آن رسم کرد.
• اصل چهارم: همه زوایای قائمه بر هم منطبق می شوند.
• اصل پنجم: از یک نقطه در خارج یک خط، یک خط و فقط یک خط می توان به موازات خط مفروض رسم کرد.

اصلاح تقویم ایرانی
زمانی که ملک شاه سلجوقی، سمرقند را فتح کرد، خیام یکی از منجمان بزرگ آن عصر بود. خواجه نظام الملک، وزیر ملک شاه، برای اصلاح تقویم رایج او را فراخواند. در گاه شماری رایج در آن زمان که گاه شماری یزدگردی بود، عدم توجه به کبیسه گیری باعث شده بود که در طول سال ها، اعتدال بهاری (نوروز) به جای اول فروردین با نوزدهم فروردین منطبق شود. همچنین با ورود اسلام به ایران، تقویم هجری قمری رایج شد که زمان بندی گرفتن مالیات از کشاورزان را با مشکل مواجه می ساخت. به این دلیل، ملک شاه تصمیم گرفت که با تغییر تقویم به شمسی، تاریخ وصول مالیات را یکنواخت کند. خیام در راس گروهی از منجمان و ریاضیدانان بزرگ دیگر، در رصدخانه اصفهان به رصد و محاسبات نجومی پرداخت که حاصل آن تقویم امروزی جلالی بود که یکی از دقیق ترین گاه شماری جهان به شمار می رود.

دنیای امروز، خیام را بیشتر به خاطر رباعیاتش می شناسد. خیام شاعر، یک قرن پس از مرگ او کشف شد. گویا تنگ نظری های زمانه اجازه نمی داد که این روح آزاده، رباعیات سرشار از اندیشه و پرسشگری را در زمان حیات خود، منتشر کند. دورانی که خیام در آن زندگی می کرده برای اذهان آزاده و پرسشگر، دوران صعب و دشواری بوده است. زمانه ای که در آن فیلسوفان به زندقه، کفر و نامسلمانی متهم می شدند. این شرایط می توانست دلیلی باشد که خیام اشعارش را که تمام جزم ها و تعصبات را به پرسش می کشید، به عنوان جنبه خصوصی تفکر خود، پنهان و پوشیده نگاه دارد. خیام برای بیان عصاره تاملات خود قالب شعری رباعی را برگزیده است و امروز رباعی با نام او عجین شده و خیام آن را به اوج خود رسانده است.

[toggle title=”برای مشاهده منابع اینجا کلیک کنید.” state=”close” ]

مقاله علمی و آموزشی «خیام؛ پیشگام کشفیات ریاضی»، نتیجه ی تحقیق و پژوهش، گردآوری و نگارش هیئت تحریریه پورتال یو سی (شما می توانید) می باشد. در این راستا گزارش موسی توماج ایری در مجله دانشمند، به عنوان منبع اصلی مورد استفاده قرار گرفته است.

[/toggle]