روش های ساده برای محاسبات ذهنی ریاضی
تکنیک های محاسبات ذهنی، تکنیک هایی هستند که شما را قادر می سازند محاسبات ریاضی را تنها با استفاده از توانایی های مغز انجام دهید. هر فردی که به تکنیک های محاسبات ذهنی مسلط شود، می تواند بخش عمده ای از محاسبات آزمون هایی مانند کنکور و همچنین حساب و کتاب های روزانه خود را به صورت ذهنی و بدون نیاز به ابزارهای کمکی مانند ماشین حساب انجام دهد.
شاید بهترین خبر در این لحظه، این باشد که همه امکان یادگیری این تکنیک ها را دارند. تنها تفاوت افرادی که می توانند محاسبات ریاضی را در ذهن و به سرعت انجام دهند با افرادی که چنین توانایی را ندارند، در پشتکار و تمرین کردن است.
در ادامه شما می توانید با برخی از روش های ساده برای محاسبات ذهنی ریاضی آشنا شوید.
ضرب اعداد در 5 – 50 – 500 و…
یک روش ساده برای ضرب کردن هر عددی در 5 این است که عدد مورد نظر را در 10 ضرب نموده، سپس بر 2 تقسیم کنیم.
مثال: عدد 165 را در 5 ضرب کنید.
165 × 5 => 165 × 10 = 1650 ÷ 2 = 825
برای محاسبه ذهنی کافی است یک صفر سمت راست عددی که در 5 ضرب می شود قرار دهیم و سپس آن را بر 2 تقسیم کنیم. به این نکته توجه داشته باشید که برای ضرب هر عددی در 50 باید آن را در 100 ضرب کنیم سپس بر 2 تقسیم نماییم؛ یا برای ضرب هر عددی در 500 باید آن را در 1000 ضرب و سپس بر 2 تقسیم کنیم.
مثال: عدد 184 را در 5000 ضرب کنید.
خب برای حل این مثالِ به ظاهر سخت، کافی است 184 را بر 2 تقسیم کنیم که می شود: 92؛ سپس 4 تا صفر جلوی 92 قرار دهیم؛ که به این ترتیب جواب ضرب 184 در 5000 می شود: 920000.
184 × 5000 => 184 ÷ 2 = 92 × 10000 = 920000
تقسیم اعداد بر 5 – 50 – 500 و…
برای تقسیم هر عددی بر 5 می توانیم آن عدد را در 2 ضرب نموده و سپس بر 10 تقسیم کنیم.
مثال: حاصل تقسیم 140 بر 5 را بیابید.
140 ÷ 5 => 140 × 2 = 280 ÷ 10 = 28
برای تقسیم هر عددی بر 50، می توان آن عدد را در 2 ضرب نمود و سپس بر 100 تقسیم کرد. به همین شکل، تقسیم هر عددی بر 500، 5000 و… نیز قابل محاسبه می باشد.
ضرب اعداد در 25 – 250 – 2500 و…
دو راه ساده برای ضرب کردن هر عددی در 25 این است که:
1) عدد مورد نظر را دو بار در 5 ضرب کنیم.
مثال: حاصل ضرب 27 در 25 را بیابید.
27 × 25 => 27 × 5 = 135 × 5 = 675
2) عدد مورد نظر را در 100 ضرب نموده و سپس بر 4 تقسیم کنیم. به عبارتی دیگر، برای ضرب هر عددی در 25، کافی است دو صفر سمت راست آن عدد قرار دهیم، سپس آن را بر 4 تقسیم نماییم.
مثال: حاصل ضرب 14 در 25 را بیابید.
14 × 25 => 1400 ÷ 4 = 350
به همین صورت اگر حاصل ضرب عددی در 250 یا 2500 و… مورد نظر باشد، می توان آن عدد را در 25 ضرب کرد و یک یا دو صفر و… به سمت راست عدد بدست آمده، اضافه نمود.
مثال: حاصل ضرب 245 در 2500 را محاسبه کنید.
245 × 2500 => (245 × 25) × 100 = (24500 ÷ 4) × 100 = 612500
یا
245 × 2500 => ((245 × 5) × 5) × 100 = (1225 × 5) × 100 = 612500
تقسیم اعداد بر 25 – 250 – 2500 و…
برای تقسیم هر عددی بر 25، می توان آن را در 4 ضرب نمود، سپس بر 100 تقسیم کرد.
مثال: 625 را بر 25 تقسیم کنید.
625 ÷ 25 => 625 × 4 = 2500 ÷ 100 = 25
برای تقسیم هر عددی بر 250 یا 2500 و… کافی است آن عدد را در 4 ضرب نموده و بر 1000 یا 10000 و… تقسیم کنیم.
مثال: حاصل تقسیم 4560 بر 2500 را محاسبه کنید.
4560 ÷ 2500 => 4560 × 4 = 18240 ÷ 10000 = 1.824
ضرب عدد دو رقمی بین 10 و 20 در خودش
برای ضرب دو عدد دو رقمی که بین 10 و 20 قرار دارند، ابتدا باید به این نکته توجه داشت که نتیجه، عددی سه رقمی بین 100 و 400 می باشد. حالا برای پیدا کردن حاصل ضرب اعداد دو رقمی بین 10 و 20 در خودش به روش زیر عمل می کنیم:
1) رقم یکان آن دو عدد را در هم ضرب می کنیم، اگر حاصل یک رقمی بود، آن را به عنوان اولین رقم سمت راست می نویسیم و اگر دو رقمی است، رقم یکان آن را نوشته، دهگان آن را در حافظه ی خود نگه می داریم.
2) رقم یکان آنها را با هم جمع می کنیم و اگر دهگانی از قبل داشته باشیم به آن افزوده، به عنوان دومین رقم ثبت می نماییم. در اینجا هم اگر رقم بدست آمده، دهگانی داشته باشد، به حافظه می سپاریم.
3) رقم دهگان آنها را در هم ضرب می کنیم و در صورتی که از قبل دهگانی در حافظه داشته باشیم با آن جمع نموده، به عنوان سومین رقم در کنار رقم های قبلی می نویسیم.
مثال: عدد 13 را در خودش ضرب نمایید.
- حاصل ضرب (3 × 3) رقم یکان را تشکیل می دهد.
- حاصل جمع (3 + 3) رقم دهگان را تشکیل می دهد.
- حاصل ضرب (1 × 1) رقم صدگان را تشکیل می دهد.
- و نتیجه می شود:
13 × 13 = 169
مثال: حاصل ضرب 14 × 14 را بدست آورید.
- حاصل ضرب (4 × 4) می شود 16، 6 را به عنوان رقم یکان نوشته، 1 را در حافظه نگه می داریم.
- حاصل جمع (4 + 4) می شود 8، آن را با عدد 1 قبلی جمع می کنیم، حاصل عدد 9، رقم دهگان را تشکیل می دهد.
- حاصل ضرب (1 × 1) برابر با 1 خواهد بود که رقم صدگان را مشخص می نماید.
- و نتیجه می شود:
14 × 14 = 196
مثال: 19 × 19 را محاسبه نمایید.
- حاصل ضرب (9 × 9) می شود 81، 1 را به عنوان رقم یکان نوشته، 8 را در حافظه نگه می داریم.
- حاصل جمع (9 + 9) می شود 18، بعلاوه 8 قبلی می شود 26؛ 6 را به عنوان رقم دهگان نوشته و 2 را در حافظه نگه می داریم.
- حاصل ضرب (1 × 1) برابر با 1 خواهد بود که با 2 قبلی جمع می شود و حاصل آن 3، رقم صدگان را مشخص می نماید.
- و نتیجه می شود:
19 × 19 = 361
ضرب اعداد دو رقمی مختوم به 5 در خودشان
برای پیدا کردن حاصل ضرب این گونه اعداد باید به این نکته توجه نمود که نتیجه، عددی سه یا چهار رقمی است و دو رقم سمت راست حاصل ضرب این نوع اعداد، همیشه 25 خواهد بود. به این ترتیب برای پیدا کردن حاصل ضرب به روش زیر عمل می کنیم:
به رقم دهگان یکی از اعداد، یک واحد اضافه می کنیم (a + 1) و سپس در رقم دهگان دیگری ضرب می نماییم. [a × (a + 1)] در نهایت حاصل ضرب را نوشته و یک عدد 25 در سمت راست آن قرار می دهیم. به این شکل:
a5 × a5 = [a × (a + 1)] 25
مثال: حاصل ضرب 35 × 35 را محاسبه کنید.
- یک واحد به 3 افزوده، در 3 ضرب می کنیم. 12 = 3 × (1 + 3)
- حاصل 12 می باشد. سپس 25 را در سمت راست آن قرار می دهیم.
- جواب می شود: 1225
35 × 35 => (3 + 1)(3) = 12 => 1225
مثال: حاصل ضرب 85 × 85 را پیدا کنید.
85 × 85 => (8 + 1)(8) = 72 => 7225
ضرب دو عدد با استفاده از اتحاد مزدوج
در ضرب دو عدد، گاهی می توان از اتحاد مزدوج [a2 – b2 = (a – b)(a + b)] استفاده نمود و جواب را بدست آورد. زمانی که فاصله ی اضافی و نقصانی دو عدد نسبت به عدد مختوم به صفر مثل 100 یا 1000 یا 50 و… به یک اندازه باشد، می توان از این اتحاد استفاده نمود و پاسخ را محاسبه کرد.
مثال: حاصل ضرب 99 × 101 را پیدا کنید.
چون فاصله هر دو عدد نسبت به 100 به یک اندازه می باشد، از اتحاد مزدوج استفاده می کنیم.
101 × 99 => (100 + 1)(100 – 1) = 10000 – 1 = 9999
مثال: حاصل ضرب 1003 × 997 را محاسبه کنید.
997 × 1003 => (1000 + 3)(1000 – 3) = 1000000 – 9 = 999991
مثال: حاصل ضرب 10005 × 9995 را محاسبه کنید.
9995 × 10005 => (10000 + 5)(10000 – 5) = 100000000 – 25 = 99999975
مثال: حاصل ضرب 59 × 61 را پیدا کنید.
61 × 59 => (60 + 1)(60 – 1) = 3600 – 1 = 3599
مجذور نمودن اعداد با استفاده از اتحاد اول و دوم
اتحاد اول و اتحاد دوم یادتان هست؟
اتحاد اول => (a + b)2 = a2 + b2 + 2ab
اتحاد دوم => (a – b)2 = a2 + b2 – 2ab
برای مجذور کردن اعدادی که نزدیک به اعداد مختوم به صفر باشند، می توان از این اتحادها استفاده نمود و به صورت ذهنی پاسخ را پیدا کرد. در این گونه موارد باید بتوان عدد مورد نظر را که قرار است مجذور شود، تبدیل به مجموع یا تفاضل دو عددی نمود که لااقل یکی مختوم به صفر باشد، سپس با استفاده از فرمول پاسخ را مشخص نمود. به مثال زیر توجه کنید.
مثال: عدد 1001 را به توان 2 برسانید.
فرض می کنیم 1000 = a و 1 = b باشد. بنابراین با استفاده از اتحاد اول می توان نوشت.
10012 => (1000 + 1)2 = 1000000 + 1 + 2000 = 1002001
مثال: مجذور 1999 را بدست آورید.
فرض می کنیم 2000 = a و 1 = b باشد؛ بنابراین با استفاده از اتحاد دوم، می توان نوشت.
19992 => (2000 – 1)2 = 4000000 + 1 – 4000 = 3996001
تعیین باقیمانده ی تقسیم اعداد بر 2 تا 11
اگر بخواهیم ببینیم در عدد a چند عدد b وجود دارد، باید a را بر b تقسیم کنیم. در این شرایط، a را مقسوم و b را مقسوم علیه می نامند. از تقسیم این دو، عددی مانند q به نام خارج قسمت به دست می آید که نشانگر تعداد bهایی است که در a وجود دارد و همچنین ممکن است باقیمانده ای کوچکتر از مقسوم علیه داشته باشد که آن را با r نمایش می دهیم. این رابطه a = b × q + r وقتی درست است که r < b باشد. در صورتی که 0 = r باشد، آنگاه می توان گفت که a بر b قابل تقسیم است، مثل 76 که بر 2 قابل تقسیم می باشد و باقیمانده آن صفر است. اما 77 بر 2 قابل قسمت (تقسیم) نمی باشد و باقیمانده ی آن مخالف صفر است.
قابلیت تقسیم بر 2: عددی به 2 قابل قسمت است که رقم یکان آن زوج یا صفر باشد. چنانچه آخرین رقم سمت راست یک عدد فرد باشد، نتیجه می گیریم که آن عدد بر 2 قابل قسمت نیست و باقیمانده اش یک می باشد.
مثال: آیا 421 بر 2 قابل قسمت می باشد.
چون آخرین رقم سمت راست این عدد فرد است؛ بنابراین، بر 2 قابل قسمت نیست و باقیمانده ی آن یک می باشد.
مثال: آیا 718 بر 2 قابل قسمت می باشد؟
چون آخرین رقم سمت راست آن زوج است، پس به 2 قابل قسمت بوده و باقیمانده ی تقسیم 718 بر 2، صفر می باشد.
قابلیت تقسیم بر 3: عددی بر 3 قابل قسمت است که مجموع ارقامش بر 3 قابل تقسیم باشد. در این صورت باقیمانده ی تقسیم آن عدد بر 3، صفر می باشد. چنانچه عددی بر 3 قابل قسمت نباشد، باقیمانده ی آن عدد بر 3، یک یا دو می باشد. برای پیدا کردن باقیمانده ی عددی که به 3 قابل قسمت نیست، باید از مجموع ارقام آن، مضرب های 3 را کسر نمود.
مثال: آیا 231 بر 3 قابل قسمت می باشد؟
چون 6 = 1 + 3 + 2 است و عدد 6 مضرب 3 می باشد (6 = 2 × 3)، پس این عدد به 3 قابل قسمت است و باقیمانده ی آن صفر می باشد.
مثال: آیا 322 بر 3 قابل قسمت می باشد؟
چون 7 = 2 + 2 + 3، مضرب 3 نیست پس عدد 322 بر 3 قابل قسمت نمی باشد. برای تعیین باقیمانده، کافی است نزدیکترین مضرب 3 را از مجموع ارقام آن کم نماییم. 1 = 6 – 7 یا 7 را بر 3 تقسیم کرد، تا باقیمانده ی یک بدست آید.
قابلیت تقسیم بر 4: عددی به 4 قابل قسمت است که دو رقم سمت راست آن صفر یا بر 4 قابل قسمت باشد. چنانچه عددی بر 4 قابل قسمت نباشد، باقیمانده ی تقسیم آن عدد بر 4 عدد 1، 2 یا 3 می باشد. برای یافتن باقیمانده عددی که به چهار قابل قسمت نباشد، باید نزدیکترین عدد مضرب 4 را از آن عدد کم نمود تا باقیمانده ای کوچکتر از 4 بدست آید.
مثال: آیا 5124 به 4 قابل قسمت می باشد؟
چون 24 به 4 قابل قسمت است، پس 5124 به 4 قابل قسمت می باشد و باقیمانده ی تقسیم آن بر 4، صفر است.
مثال: آیا عدد 7243 به 4 قابل قسمت می باشد؟
از آنجا که 43 به 4 قابل قسمت نیست بنابراین عدد 7243 به 4 قابل قسمت نمی باشد. روشن است که باقیمانده ی تقسیم 43 بر 4 عددی بجز 3 نمی باشد.
روش دیگر این است که رقم یکان را در 20 و رقم دهگان را در 21 ضرب نموده و حاصل آنها را با هم جمع می نماییم. اگر حاصل بزرگتر و یا مساوی 4 باشد مضارب 4 را از آن کم نموده تا مانده به کمتر از چهار برسد.
(3 × 20) + (4 × 21) = 3 + 8 = 11
11 – 8 = 3
قابلیت تقسیم بر 5: عددی بر 5 قابل قسمت است که رقم اول سمت راست آن صفر یا پنج باشد، در غیر این صورت، آن عدد بر 5 قابل قسمت نیست. برای تعیین باقیمانده ی آن عدد بر 5 کافی است به رقم اول سمت راست آن توجه کنیم. اگر این رقم از 5 کوچکتر است، پس باقیمانده ی تقسیم آن عدد بر 5، خود این عدد می باشد. ولی اگر این رقم بیشتر از 5 باشد باید 5 واحد از آن کم کرد تا باقیمانده ی تقسیم آن عدد بر 5 مشخص گردد.
مثال: آیا عدد 465 به 5 قابل قسمت است؟
چون رقم اول سمت راست آن 5 می باشد، پس این عدد به 5 قابل قسمت است و باقیمانده ی تقسیم آن بر 5، صفر می باشد.
مثال: آیا عدد 7538 به 5 قابل قسمت است؟
از آنجا که رقم اول سمت راست آن صفر یا پنج نمی باشد، پس این عدد بر پنج قابل قسمت نیست و باقیمانده ی آن بر 5 برابر با 3 می باشد. زیرا 3 = 35 – 38.
قابلیت تقسیم بر 6: عددی بر 6 قابل قسمت است که هم بر 2 و هم بر 3 قابل تقسیم باشد. در این صورت باقیمانده ی تقسیم آن عدد بر 6، صفر می شود. اگر عددی بر 6 قابل قسمت نباشد، باقیمانده ی تقسیم آن بر 6، عددی کوچکتر از 6 می باشد. برای پیدا کردن باقیمانده کافی است نزدیکترین مضرب 6 را از آن عدد کم نمود تا باقیمانده بدست آید.
مثال: آیا عدد 7671 بر 6 قابل قسمت است؟
با توجه به اینکه این عدد، زوج نیست پس بر 2 قابل قسمت نمی باشد. در نتیجه بر 6 نیز قابل قسمت نخواهد بود. برای پیدا کردن باقیمانده کافی است عدد 7668 را که نزدیکترین مضرب 6 به این عدد است را از آن کم کنیم. 3 = 7668 – 7671
مثال: آیا عدد 432 بر 6 قابل قسمت است؟
از آنجا که این عدد زوج است، پس بر 2 قابل قسمت می باشد. از طرفی مجموع ارقامش (9 = 2 + 3 + 4) 9 می باشد که بر 3 قابل قسمت است. در نتیجه این عدد بر 6 قابل قسمت بوده و باقیمانده ی آن صفر است.
قابلیت تقسیم بر 7: عددی بر 7 قابل قسمت است که باقیمانده ی آن بر 7، صفر باشد. برای اینکه باقیمانده ی تقسیم عدد a بر 7 را بدست آوریم، به شرح زیر عمل می کنیم:
اولین رقم سمت چپ عدد مورد نظر را سه برابر کرده، با رقم بعدی جمع می نماییم. سپس مضرب های 7 آن را کسر نموده، باقیمانده را سه برابر کرده و با رقم بعدی جمع می کنیم. پس از کسر مضارب هفت از آن، مجدداً به همین روش ادامه می دهیم تا باقیمانده ی نهایی حاصل شود.
مثال: باقیمانده ی تقسیم عدد 5472 بر 7 را پیدا کنید.
رقم 5 را سه برابر نموده، با 4 جمع می کنیم.
5 × 3 = 15
15 + 4 = 19
مضرب 7 یعنی 14 را از آن کم می کنیم؛ باقیمانده 5 می شود.
19 – 14 = 5
5 را سه برابر نموده، با 7 جمع می کنیم.
5 × 3 = 15
15 + 7 = 22
مضرب هفت یعنی 21 را از آن کسر می نماییم.
22 – 21 = 1
نتیجه یعنی 1 را سه برابر نموده و با 2 جمع می کنیم.
1 × 3 = 3
3 + 2 = 5
عدد 5 حاصل می شود که باقیمانده تقسیم عدد 5472 بر 7 می باشد.
مثال: آیا عدد 1813 به 7 قابل قسمت می باشد؟
1 × 3 = 3
3 + 8 = 11
11 – 7 = 4
4 × 3 = 12
12 + 1 = 13
13 – 7 = 6
6 × 3 = 18
18 + 3 = 21
21 – 21 = 0
نتیجه صفر می شود؛ پس عدد 1813 بر 7 قابل قسمت است و باقیمانده آن بر 7، صفر می باشد.
قابلیت تقسیم بر 8: عددی بر 8 قابل قسمت است که عدد متشکل از سه رقم اول سمت راست آن، به هشت قابل قسمت باشد، و یا سه رقم سمت راست آن صفر باشد.
برای پیدا کردن باقیمانده ی تقسیم عدد a، بر 8 کافی است باقیمانده ی سه رقم اول سمت راست عدد را بر 8 حساب کنیم. یعنی رقم یکان را در 20، رقم دهگان را در 21 و رقم صدگان را در 22 ضرب نموده و حاصل آنها را با هم جمع می کنیم، در صورتی که حاصل بزرگتر یا مساوی 8 باشد، مضارب 8 را از آن کم نموده تا مانده به کمتر از 8 برسد.
مثال: آیا عدد 1848 به 8 قابل قسمت است؟
از آنجا که 848 به 8 قابل قسمت است، پس 1848 نیز به 8 قابل قسمت می باشد. برای پیدا کردن باقیمانده ی 848 به 8، اولین رقم سمت چپ را با 8 مقایسه می کنیم تا در صورتی که بزرگتر یا مساوی 8 باشد، 8 را از آن کسر نماییم، سپس باقیمانده را با رقم بعدی یعنی 4 کنار هم قرار داده، مجدداً مضرب 8 را از آن کم می کنیم و بالاخره باقیمانده را با آخرین رقم یعنی 8 کنار هم قرار می دهیم و مضرب 8 را از آن کم می کنیم. رقم باقیمانده، تقسیم آن عدد بر 8 را مشخص می کند.
مثال: آیا عدد 5473000 به 8 قابل قسمت است؟
چون سه رقم راست آن صفر است، پس به 8 قابل قسمت بوده و باقیمانده ی تقسیم 5473000 بر 8، برابر با صفر می باشد.
مثال: آیا عدد 7455 به 8 قابل قسمت می باشد؟
چون 455 عدد فرد است به 8 قابل قسمت نیست، پس 7455 نیز به 8 قابل قسمت نمی باشد. اما برای یافتن باقیمانده که عددی بزرگتر از صفر و کمتر از 8 می باشد، لازم است نزدیکترین عدد سه رقی مضرب 8 به 455 را پیدا نمود و از 455 کم کرد که آن عدد 448 است.
455 – 448 = 7
بنابراین باقیمانده ی تقسیم عدد 7455 بر 8، برابر با 7 می باشد.
روش دیگر محاسبه باقیمانده این است که رقم یکان را در 20، رقم دهگان را در 21 و رقم صدگان را در 22 ضرب نموده و حاصل آنها را با هم جمع کنیم.
(5 × 20) + (5 × 21) + (4 × 22) = 5 + 10 + 16 = 31
چون رقم 31 بزرگتر از 8 می باشد 24 (نزدیکترین مضرب 8 به 31) را از آن کم می کنیم.
31 – 24 = 7
مجدد مشاهده می کنید که باقیمانده تقسیم عدد 7455 بر 8 برابر با 7 می باشد.
قابلیت تقسیم بر 9: عددی به 9 قابل قسمت است که مجموع ارقامش به 9 قابل قسمت باشد. بدیهی است اگر از مجموع ارقامش نزدیکترین مضرب 9 را کسر کنیم و باقیمانده، عددی کوچکتر از 9 شود، این عدد، باقیمانده ی تقسیم بر 9 می باشد.
مثال: آیا 2934 به 9 قابل قسمت است؟
مجموع ارقام آن عدد را محاسبه می نماییم:
2 + 9 + 3 + 4 = 18
چون 18 مضرب 9 می باشد، پس 2934 به 9 قابل قسمت است.
مثال: آیا 5376 به 9 قابل قسمت است؟
مجموع ارقام آن عدد را محاسبه می نماییم:
5 + 3 + 7 + 6 = 21
نزدیکترین مضرب 9 را از آن کم می نماییم.
21 – 18 = 3
پس این عدد به 9 قابل قسمت نمی باشد و باقیمانده ی تقسیم آن عدد بر 9 برابر با 3 می باشد.
قابلیت تقسیم بر 10: عددی به 10 قابل قسمت است که اولین رقم سمت راست آن صفر باشد. بدیهی است اگر رقم سمت راست آن، رقمی غیر از صفر باشد، همان رقم باقیمانده ی تقسیم آن عدد بر 10 می باشد.
مثال: آیا 2654 بر 10 قابل قسمت می باشد؟
چون اولین رقم سمت راست آن صفر نیست، پس این عدد بر 10 قابل قسمت نمی باشد و باقیمانده ی تقسیم آن بر 10، 4 می باشد. زیرا اولین رقم سمت راست آن 4 است.
مثال: آیا 5670 بر 10 قابل قسمت می باشد؟
چون رقم اول سمت راست آن عدد صفر است، پس بر 10 قابل قسمت می باشد و باقیمانده ی آن صفر خواهد بود.
قابلیت تقسیم بر 11: فرض کنیم عدد صحیح A شامل n رقم باشد. مکان ارقام A را از راست به چپ به ترتیب زوج و فرد در نظر می گیریم و سپس ارقام در مکان های زوج را با هم جمع کرده، منهای مجموع ارقام مکان های فرد می کنیم، اگر باقیمانده صفر باشد، عدد بر 11 قابل قسمت است. ولی اگر باقیمانده مثبت و کمتر از 11 بود، همان عدد باقیمانده ی تقسیم عدد A بر 11 می باشد. حالا اگر باقیمانده منفی و یا مثبت و بزرگتر از 11 بود، آنگاه باید مضرب 11 را به آن اضافه یا کم نمود تا باقیمانده ی واقعی که کوچکتر از 11 می باشد، بدست آید.
مثال: بررسی کنید که عدد 27493 بر 11 بخش پذیر می باشد یا خیر؟
ارقام در مکان های زوج را با هم و ارقام در مکان های فرد را نیز با هم جمع می نماییم. تفاوت آنها 7- می باشد. با اضافه کردن 11 به آن، نتیجه 4 می شود.
(3 + 4 + 2) – (9 + 7) = 9 – 16 = -7
-7 + 11 = 4
پس این عدد بر 11 قابل قسمت نیست و باقیمانده ی تقسیم آن بر 11، 4 می باشد.
مثال: آیا 11935 بر 11 قابل قسمت می باشد؟
(5 + 9 + 1) – (3 + 1) = 15 – 4 = 11
چون 11 مضرب 11 می باشد، پس 11935 به 11 قابل قسمت است و باقیمانده ی این تقسیم، صفر می باشد.
ساده کردن کسر
اگر صورت و مخرج کسری، دارای عامل مشترکی مخالف صفر و غیر از یک باشند، می توانیم آنها را بر آن عامل مشترک تقسیم کنیم. به عبارت دیگر، برای ساده کردن کسر باید صورت و مخرج آن را جداگانه به عوامل ضرب تجزیه نموده، سپس در صورت اشتراک عوامل ضرب مخالف صفر بین صورت و مخرج، آنها را حذف کرد.
بدیهی است چنانچه هیچ عامل مشترکی بین صورت و مخرج به جزء 1 نباشد، نتیجه می گیریم که این کسر ساده نمی شود. به این نوع کسرها، کسر تحویل ناپذیر گویند.
مثال: کسر 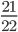 را ساده کنید.
را ساده کنید.
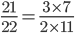
چون در صورت و مخرج کسر هیچ عامل مشترکی دیده نمی شود این کسر تحویل ناپذیر است و ساده نمی شود.
مثال: کسر 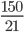 را ساده کنید.
را ساده کنید.
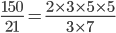
تنها عامل مشترک بین صورت و مخرج 3 می باشد، پس از حذف عدد 3 از صورت و مخرج، جواب می شود: 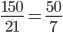
مثال: کسر 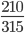 را ساده کنید.
را ساده کنید.
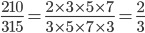
عوامل مشترک 3، 5، 7 بین صورت و مخرج قابل حذف کردن می باشند. بنابراین با حذف آنها کسر 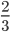 حاصل می گردد.
حاصل می گردد.
یادگیری تکنیک های محاسبات ذهنی ریاضی می توانند موجب افزایش قدرت ذهن، تخیل و خلاقیت، افزایش اعتماد به نفس، توسعه و بهبود عملکرد همزمان دو نیمکره مغز، مدیریت زمان و تمرکز بهتر شوند. بنابراین با پشتکار و تمرین های پیوسته، سختی ها را پشت سر بگذارید.
منابع
مقاله علمی و آموزشی «روش های ساده برای محاسبات ذهنی ریاضی»، نتیجه ی تحقیق و پژوهش، گردآوری و نگارش هیئت تحریریه پورتال یو سی (شما می توانید) می باشد. در این راستا کتاب ریاضیات امور مالی، نوشته ی رحیم افتخار از شرکت چاپ و نشر کتاب های درسی ایران، منتشر شده در 1384 به عنوان منبع اصلی مورد استفاده قرار گرفته است.




عالی
Really thanks
دستت درد نکنه بخاطر این مقاله کنکور شیمی را خوب زدم
سلام…
خیلی عالی و کاربردی، دمتون گررررررمممم…
عالیییییییییییی
سلام
ممنون از مطالب جالبتون
سلام؛ با عرض پوزش اولا خسته نباشید و ممنون بابت کارتون
ولی فک کنم نه شما بلکه هیچ شخصی در ایران نخواهد توانست و یا نخواهد خواست که تقسم مثلا 7 تقسیم بر 123 و مانند این تقسیم ها که واقعا غول دست و پا گیر هستند رو به روشی ساده اجرا کنه فقط و فقط تقسیم 5 تقسیم 10 ضرب های به درد نخور که والا خجالت آوره حتی به بچه ابتدایی بگین رو نشر میدید افسوس
… نخور اگه بلد بودی همینارو وارد ابن سایت نمیشدی دهنتم ببند گمشو برو سایت های خارجی دنبال تقسیم مزخرفت بگرد
دوست عزیز به جای اینکه فحش بدی و غیرمنطقی برخورد کنی، یکم منطقی باش. اتفاقا من کاملا با نظر اوشون موافق هستم… من تو این سایت به امید تکنیک های جدید اومدم ولی همش تکراریه و چه بسا تقسیم اعداد بر ۷ رو اگه بیایم تقسیم کنیم راحت تر از این فرمولاس! البته کاربردی هستن ولی جدید نیستن و اکثرا مطمئنم بلدن اینا رو و فقط منم وقتمو تلف کردم اومدم تو این سایت…
۱۲۳ تقسیم بر ۷ = ۱×۳ = ۳ . ۳+۲= ۵ . ۵_۰=۵
۵×۳=۱۵ . ۱۵+۳=۱۸ . ۱۸-۱۴=۴ => r=4
تو خنگی چرا بقیه رو مسئول میدونی:)
سلام خیلی عالی بود خسته نباشید
روشی هم برای تقسیم های خیلی بزرگ هم سراغ دارین؟
مثلا 8 رقمی به چهار رقمی؟؟