نیکلای لباچفسکی: مبدع هندسه غیر اقلیدسی

ابزار ریاضی لازم برای نظریه ای چون نسبیت اینشتین، وقتی فراهم شد که برخی اذهان خلاق توانستند به تصوراتی فراتر از آنچه که از زمان اقلیدس به بعد بر افکار ریاضیدانان تسلط داشت، بپردازند. پیشگام این تحول که منجر به تولید هندسه های نااقلیدسی شد، ریاضیدانی روس به نام «نیکلای ایوانوویچ لباچفسکی» بود.

در این مقاله شما می توانید با نیکلای لباچفسکی آشنا شوید.

تا زمان اقلیدس در قرن سوم پیش از میلاد، یافته های هندسه پراکنده بود و نظم و انسجام خاصی نداشت. کار بزرگ اقلیدس آن بود که تمام قضایای هندسی زمان خود را در کتابش به نام «اصول» جمع آوری و بطور منطقی و مستدل انسجام بخشید. هدف او این بود که مجموعه ای هماهنگ و منطقی از هندسه مقدماتی فراهم کند که هر قضیه آن را بتوان از قضایای قبلی نتیجه گرفت. اقلیدس که سعی کرد ضمن جمع آوری قضایای هندسی موجود، به اثبات برهانی آنها بپردازد،‌ با چهار اصل اولی که فرض کرد، توانست 28 قضیه هندسی را اثبات کند اما برای اثبات قضایای بیشتر مجبور شد اصل پنجمی را نیز اضافه کند. با اینکه هندسه اقلیدس بیش از دو هزار سال به عنوان هندسه ای سرشار از زیبایی استنتاج منطقی و سازگار با تجارب روزمره با اقبال و ستایش و اعتبار همراه بود و گالیله، کوپرنیک و نیوتن و حتی فیلسوف بزرگی چون کانت، نظریات خود را بر اساس آن بنیان نهادند، اما ابهام در ماهیت پنجم، همواره موضوع تفکر ریاضیدانان باقی ماند.

اصول موضوعه هندسه اقلیدسی

اصول موضوعه، فرضیاتی هستند که بدیهی شمرده شده و پذیرفته می شوند و مبنای اثبات سایر قضایا قرار می گیرند. اصول موضوعه هندسه اقلیدسی شامل پنج اصل زیر است:

اصل اول: از هر دو نقطه فقط یک پاره خط مستقیم می گذرد.

اصل دوم: هر پاره خط را می توان در امتداد آن بطور نامحدود ادامه داد.

اصل سوم: برای هر پاره خط دلخواه می توان دایره ای به شعاع آن پاره خط و به مرکز یک سر آن رسم کرد.

اصل چهارم: همه زوایای قائمه بر هم منطبق می شوند.

اصل پنجم: از یک نقطه در خارج یک خط، یک خط و فقط یک خط می توان به موازات خط مفروض رسم کرد.

اصل دردسرساز

بر اساس اصل پنجم اقلیدس، از یک نقطه در خارج یک خط، یک خط و فقط یک خط می توان به موازات خط مفروض رسم کرد. چند مسئله باعث شد که پذیرش اصل پنجم یا اصل توازی برای ریاضیدانان بعدی دشوار باشد. یکی اینکه این اصل بداهت و ایجاز چهار اصل اول را نداشت. دوم اینکه این اصل بیشتر به یک قضیه شباهت داشت تا یک اصل موضوعه،‌ سوم اینکه اقلیدس پس از اثبات 28 قضیه با چهار اصل اول و ناکامی در اثبات قضایای بیشتر با آن اصول و 28 قضیه اثبات شده، ناگزیر به افزودن اصل پنجم شد. پس از اقلیدس، ریاضیدانان بسیاری از جمله خواجه نصیر طوسی و عمر خیام به بررسی این اصل پرداختند و سعی کردند این اصل آزاردهنده را با استفاده از چهار اصل اول به اثبات برسانند. خیام در رساله «در شرح مشکلات کتاب اصول اقلیدس»‌ سعی کرد اصل توازی را اثبات کند. هر چند تلاش خیام در این زمینه ناکام ماند اما روشی که برای این منظور بکار برد، 700 سال بعد مورد توجه ریاضیدانان اروپایی قرار گرفت. آنچه که امروزه در هندسه به «چهار ضلعی خیام – ساکری» معروف است، بیانگر تلاش خیام برای اثبات اصل پنجم اقلیدس است.

هندسه اقلیدسی در طول قرن ها آنچنان اعتباری یافته بود که ادعای فرضی بر خلاف مفروضات آن،‌ حرکتی بسیار جسورانه و انقلابی و از طرفی جنون آمیز و حماقت بار محسوب می شد. اما تاریخ علم نمونه های بسیاری از نظریات جنون آمیز را ثبت کرده که در نهایت به انقلابی در علم منجر شده و مورد پذیرش عمومی قرار گرفته اند. شاید از این رو است که اینشتین گفته «به ایده ای که در نگاه اول احمقانه به نظر نرسد، امیدی نیست». بالاخره پس از گذشت دو هزار سال، ایده ای از این نوع به تولد جهان های جدیدی در هندسه منجر شد.

پیشرفت غیر عادی

نیکلای ایوانوویچ لباچفسکی دومین فرزند کارمندی معمولی بود که در اول دسامبر سال 1793 در ناحیه ماکاریف در روسیه به دنیا آمد. پدرش در هفت سالگی او درگذشت و مادرش برای سرپرستی سه کودک خود، با مشکلات مالی شدیدی روبرو شد. از این رو به شهر کازان رفت و سعی کرد هر طور شده امکان تحصیل کودکان خود را فراهم کند. تلاش او نتیجه داد و هر سه کودک او توانستند در مدرسه شبانه روزی به عنوان شاگرد مستمری بگیر پذیرفته شوند. نیکلا در هشت سالگی وارد این مدرسه شد. او بویژه در ریاضیات و ادبیات کلاسیک با سرعت غیر عادی پیشرفت کرد. در چهارده سالگی وارد دانشگاه کازان شد و چهل سال بعدی زندگی خود را با عناوین دانشجو، دانشیار، استاد و بالاخره رئیس دانشگاه در آنجا سپری کرد.

در بیست و سه سالگی استاد دانشگاه کازان شد و غیر از ریاضیات، نجوم و فیزیک نیز تدریس می کرد. او همواره با مشغله های اداری بسیاری در دانشگاه درگیر بود. از ریاست کتابخانه و موزه گرفته تا ریاست دانشگاه. در سال 1828 به ریاست دانشگاه کازان برگزیده شد. لباچفسکی در اوج قدرت فکری و شهرت علمی در سال 1846 بدون هیچ توضیحی از طرف حکومت روسیه از تمام مشاغل دانشگاهی (چه به عنوان استاد و چه به عنوان ریاست دانشگاه) عزل شد. او در اواخر عمر بینایی خود را از دست داد و در 24 فوریه 1856 در 63 سالگی در شهر کازان درگذشت.

انقلاب هندسی

بسیار  عجیب به نظر می رسد که با وجود مشغله های بسیار دانشگاهی، لباچفسکی چگونه می توانست به کار پژوهش علمی بپردازد. وی به مدت بیست سال یا بیشتر، بطور آهسته و پیوسته و هر وقت که امکانش را می یافت، به تحقیقات ریاضی پرداخت. او در سال 1826 کتابی را در دانشگاه کازان منتشر کرد که کسی به ارزشش پی نبرد تا آنکه گوس آن را در سال 1840 کشف کرد. لباچفسکی به جای اینکه برای اثبات اصل پنجم اقلیدس تلاش کند، فرض کرد که از یک نقطه در خارج خط به جای یک خط موازی با خط مفروض، دو خط به موازات آن بتوان رسم کرد و نتایج بعدی را مبتنی بر این فرض استنتاج کرد و هرچه جلوتر رفت نه تنها با هیچ تناقضی مواجه نشد بلکه در کمال شگفتی دریافت که هندسه ای جدید، هماهنگ و قائم به ذات را کشف کرده است.

وجه انقلابی کشف لباچفسکی این بود که هندسه اقلیدسی را که متفکران بزرگی چون نیوتن و کانت،‌ آن را به عنوان  حقیقتی مطلق و تنها هندسه منطبق بر واقعیت می شمردند، صرفاً به عنوان یکی از هندسه های ممکن معرفی کرد. جسارت لباچفسکی در به پرسش کشیدن مفروضاتی که در طول دو هزار سال به عنوان حقیقت مطلق انگاشته می شد و نتایج بدیع حاصل از کار وی، ریاضیدانان و دانشمندان را بر آن داشت که به سایر اصول یا حقایق پذیرفته شده حمله کرده و به نتایج جدیدی دست یابند. سی سال پس از آن بود که ریمان، هندسه غیر اقلیدسی دیگری (هندسه ریمانی یا بیضوی) را کشف کرد که مبنای نظریه نسبیت اینشتین قرار گرفت و به انقلابی در فیزیک منجر شد.

هندسه نااقلیدسی

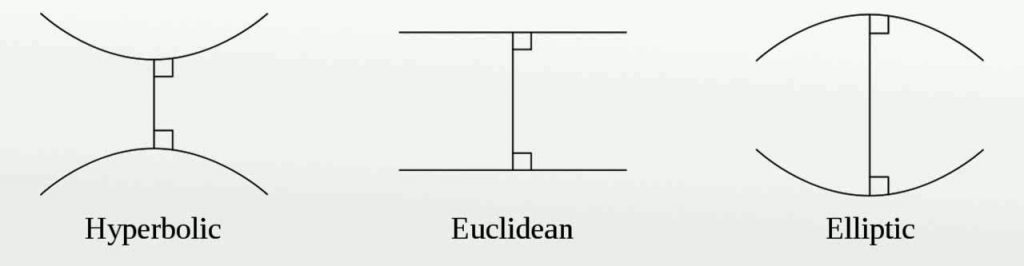
همانطور که اشاره شد، هندسه نااقلیدسی از بررسی و تلاش برای اثبات اصل پنجم اقلیدس ناشی شد. اگر دو نیم خط عمود بر یک پاره خط را مطابق شکل در نظر بگیریم، در هندسه اقلیدسی فاصله عمودی بین دو خط با حرکت به طرفین آن ثابت باقی می ماند. در هندسه های نااقلیدسی با حرکت به طرفین، فاصله مذکور تغییر می کند. بطوریکه در هندسه لباچفسکی (هندسه هذلولوی یا هیپربولیک) این فاصله افزایش می یابد و در هندسه بیضوی یا ریمانی فاصله کم می شود.

از لحاظ تجسمی می توان فرض کرد که خطوط مذکور در هندسه اقلیدسی روی سطحی با انحنای صفر، در هندسه هذلولوی روی سطحی با انحنای منفی و در هندسه بیضوی روی سطحی با انحنای مثبت قرار دارند. یانوش بویویی (ریاضیدان مجارستانی) نیز دو سال پس از لباچفسکی و بطور مستقل هندسه هذلولوی را کشف کرد و در کنار لباچفسکی به عنوان یکی از کاشفان هندسه نااقلیدسی شناخته می شود.

با این وصف و تغییر نگرشی که در معرفت بشری تحت تاثیر کشف هندسه غیر اقلیدسی توسط لباچفسکی روی داد، اغراق آمیز نیست اگر او را با عنوان «کوپرنیک جهان هندسه» توصیف کنیم.

منابع

مقاله علمی و آموزشی «نیکلای لباچفسکی: مبدع هندسه غیر اقلیدسی»، نتیجه ی تحقیق و پژوهش، گردآوری و نگارش هیئت تحریریه پورتال یو سی (شما می توانید) می باشد. در این راستا گزارش موسی توماج ایری در مجله دانشمند، به عنوان منبع اصلی مورد استفاده قرار گرفته است.